回文数判断 Palindrome Number
题目
判断一个整数是否是回文数。回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
以下为详细说明:
Determine whether an integer is a palindrome. An integer is a palindrome when it reads the same backward as forward.
Example 1:
Input: 121
Output: true
Example 2:
Input: -121
Output: false
Explanation: From left to right, it reads -121. From right to left, it becomes 121-. Therefore it is not a palindrome.
Example 3:
Input: 10
Output: false
Explanation: Reads 01 from right to left. Therefore it is not a palindrome.
Follow up:
Coud you solve it without converting the integer to a string?
思路&题解
回文现象不仅在数字中存在,字符串中也存在,注意题目要求,不同通过转换为字符串来解答问题。
本题和整数翻转有点相似的地方是按位处理数字,但是差异点也有,比如需要区分正负问题,负数不存在回文,因为符号回文后不是一个合法数字。 暴力解法是,将整个数从低位开始,逐一翻转,最后对比一下翻转后的数字和源数字是否相等。
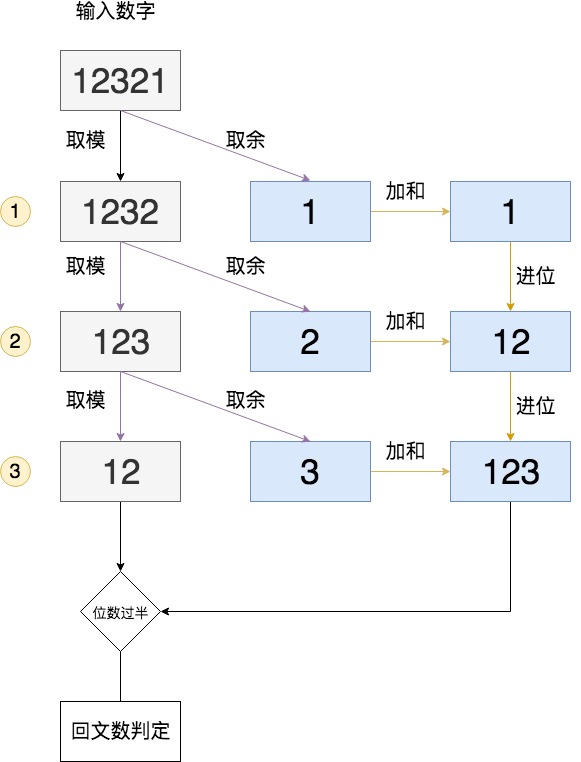
整个解法虽然可行,但是有冗余计算的嫌疑,我分仔细看一下回文规律:
实际上只需要按位处理到数值的中间位,然后对比左右两侧的数字,就可以知道是不是回文数
除此之外,在考虑有没有特殊值需要排除:
- 负数排除
- 个位数是0的多位数排除
- 0本身是回文数
public class Solution {
public boolean isPalindrome(int x) {
// 易错点:特殊值需要提前排除
if(x < 0 || (x%10 == 0 && x != 0)){
return false;
}
int result = 0;
// 易错点:判断位数达到一半
while(x > result) {
result = result*10 + x%10;
x /= 10;
}
// 易错点:对半判断
return result == x || result/10 == x;
}
}
知识点分析
梳理一下这题的几个知识点。
回文数的规律&特殊值 负数排除是比较直观的,但是10的倍数也需要排除。除了0之外,由于整数高位不能是0,因此个位数是0的整数翻转后不是回文数。
如何判断位数的一半
针对字符串,我们可以很简单就感知到长度的1/2,但是针对一个数字,没有长度这个属性维度,如果要判断1/2,那么可以通过间接比较不同位数数值大小的方式来判定。 举例来说,3位的数值肯定大于2位的,因此当按位处理,发现待处理部分已经小于处理部分的翻转值之后,我们可以认为已经达到1/2,或者超过1/2+1位。
抛一个问题,如果不排除个位数是0的数值,那么按位处理逻辑如何保证正确性?
前面判定1/2的逻辑,由于我们不能精确识别1/2,只得出了1/2和1/2+1的位置,因此最后判断对半的时候是有些问题的:
假设x是100,我们处理过后,x=0,result=1时才能打破循坏,此时位数关系已经不满足1/2,或者1/2+1, 如果继续比较,能够命中result/10==x的判断,显然100不是回文数,计算结果是错误的。
如果要精确判定1/2,还有一种办法,通过循环计算,不断的除以10,来计算书数值的位数:
// TODO 需要考虑溢出问题
int num = 10000;
int count = 1;
while ((num / (int)Math.pow(10, count)) > 0) {
count++;
}
System.out.println(num + "=>" + count);